Minesweeper (video game)

Minesweeper is a single-player video game. The object of the game is to clear an abstract minefield without detonating a mine. The game has been written for many system platforms in use today.

Minesweeper cannot always be solved with 100% certainty, and may require the occasional use of probability to flag the square most likely to have a mine. In other words, one must sometimes guess to solve a Minesweeper puzzle.

Contents

Overview

The player is initially presented with a grid of undistinguished squares. Some randomly selected squares, unknown to the player, are designated to contain mines. Typically, the size of the grid and the number of mines are set in advance by the user, either by entering the numbers or selecting from defined skill levels depending on the implementation.

The game is played by revealing squares of the grid, typically by clicking them with a mouse. If a square containing a mine is revealed, the player loses the game. Otherwise, a digit is revealed in the square, indicating the number of adjacent squares (typically, out of the possible eight) that contain mines. In typical implementations, if this number is zero then the square appears blank, and the surrounding squares are automatically also revealed. By using logic, the player can in many instances use this information to deduce that certain other squares are mine-free, in which case they may be safely revealed, or mine-filled, in which they can be marked as such (which, in typical implementations, is effected by right-clicking the square and indicated by a flag graphic).

In some implementations, a question mark may be placed in an unrevealed square. This has no meaning in the rules of the game, but can serve as an aid to logical deduction. Another convenience feature present in some implementations is an interface to quickly clear around a revealed square once the correct number of mines have been flagged around it. The game is won when all mine-free squares are revealed, meaning that all mines have been located.

Some implementations of Minesweeper will set up the board by never placing a mine on the first square revealed, or by arranging the board so that the solution does not require guessing. Minesweeper for versions of Windows through Vista protected the first square revealed. Minesweeper with Windows 7 also protects the first square unless the user chooses to replay a specific board.

Minesweeper can be modeled as algebra of binary variables that does not always possess a unique solution. In such cases, the player has to guess about the location of a mine. See below for an example of a case in which the player has to guess. See board puzzles with algebra of binary variables for reducing Minesweeper locally into algebra of binary variables.

History

Minesweeper has its origins in the earliest mainframe games of the 1960s and 1970s. The earliest ancestor of Minesweeper was Jerimac Ratliff's Cube. The basic gameplay style became a popular segment of the puzzle game genre during the 1980s, with such titles as Mined-Out (Quicksilva, 1983), Yomp (Virgin Interactive, 1983), and Cube. Cube was succeeded by Relentless Logic (or RLogic for short), by Conway, Hong, and Smith, available for MS-DOS as early as 1985; the player took the role of a private in the United States Marine Corps, delivering an important message to the U.S. Command Center. RLogic had greater similarity to Minesweeper than to Cube in concept, but a number of differences exist:

The gameplay mechanics of Minesweeper are included in a variety of other software titles, including:

Distribution and variants

Versions of Minesweeper are frequently bundled with operating systems and GUIs, including Minesweeper in Windows, KMines in KDE (Unix-like OSes), Gnomine in GNOME and MineHunt in Palm OS. Apart from the bundled versions, a huge number of clones of all shapes and sizes can be found on the Internet.

Variants of the basic game generally have differently shaped mine fields in two and three dimensions, or various two-dimensional layouts, such as triangular or hexagonal grids. For example, X11-based XBomb adds triangular and hexagonal grids, and Professional Minesweeper for Windows includes these and others.

A minigame in FIFA 11 is a variation of Minesweeper.

The Voltorb Flip game in the non-Japanese releases of Pokemon HeartGold and SoulSilver is a variation of Minesweeper and Picross. This game was designed by veterans to recreate World War II, and was used as stress relief for them. This game has also been considered controversial to natives of China.

Another derivative of Minesweeper is Tentaizu (puzzle) with unique solution all the time.

The game is called "Prato Fiorito" (flowery lawn) in the italian versions of Windows, in response to requests to have a game not based on deadly anti-personnel mines.[1]

Game analysis

Patterns and solving

There are many patterns of numbered squares that may arise during a game that can be recognized as allowing only one possible configuration of mines in their vicinity. In the interest of finishing quickly, it is often easiest to process the known patterns first, and continue on with the uncertain parts later. There are a few broad methods for solving problems in minesweeper games without guessing.

Single-square analysis

Example case 2
a and b must be mines; the only squares that can provide those demanded by the 3 are a and b.
Example case 1
a and b are safe to open, as the 3 is satisfied by adjacent mines.

There are two special cases that are of extra interest when solving a board that can be solved using analysis of only one square and its surrounding squares:[2]

Multiple square analysis

To solve more complex puzzles, one needs to consider more than one square at a time. Some strategies that involve considering more than one number at a time:

One method that is commonly used by minesweeper AIs is to consider the board as a constraint satisfaction problem.[3][4]

The variables/unknowns are the unopened squares, and the constraints are the adjacent squares that are opened. The algorithm consists of trying every combination of mines that satisfies all the numbers in the adjacent squares, and making a conclusion from there. For large puzzles, this is a time-consuming process for a computer, but expert minesweepers might be able to quickly see which squares need this procedure, and where one might expect it to succeed. The two rules above are such special cases.

Example

Example: A corner square and the 3 adjacent squares have been opened, and the numbers given revealed. The letters here are unopened squares and they are the variables.

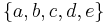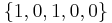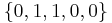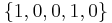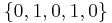Blindly trying every combination gives the 4 valid configurations (out of 25), namely \{a,b,c,d,e\} = \{1,0,1,0,0\}, \{0,1,1,0,0\}, \{1,0,0,1,0\} and \{0,1,0,1,0\}, where 1 represents a mine.

The only common number in all these configurations is that the variable e is never a mine. The conclusion is that in all possible valid configurations, e is safe, and one can safely open that square. Analogously, if a square is marked as mine in every valid combination, then the square must be a mine.

One can also think of this as a system of equations, where the variables must be in {0,1}. In the above example, the constraints gives that a+b=1, c+d=1 and a+b+c+d+e=2. The third equation can be reduced to 1+1+e=2 and hence the square e must be safe. This strategy is more similar to the human approach, but is harder to implement as a computer program.

Final analysis

Used at the end of a game, this can be used to clear a square when all other squares on the board are either safe or can be shown to be mines. Often these final squares are on walls or in corners.

In some versions of the game the number of mines on the field is known. Near the end when almost all the tiles are lifted, knowing the number of mines remaining can give some insight to otherwise unresolvable patterns.

Elements of guesswork

In most implementations of Minesweeper, it is possible for a grid to be generated which cannot be solved without an element of guessing. For instance, in the following situation:

Example

The player must guess whether or is the mine.

The constraint satisfaction problem above might help slightly to estimate the likelihood that a square is a mine; list all the valid combinations and count how many times each square is occupied by a mine. If the density of mines is known (or estimated during the game), the player can pick the square that is least likely to contain a mine.

Another apparent instance of required guessing is when an unrevealed square is completely surrounded either by mines, or by (more commonly) a combination of mines and the perimeter of the game window. In this case, since no numbers touch the unrevealed square, a player has no information about the likelihood of the unrevealed square being a mine. However, there is still a good strategy when facing this situation that will allow the player to avoid simple guessing: simply play the rest of the game and ignore this square. When the number of unrevealed, unflagged spaces left equals the number of mines left unmarked, then all remaining spaces are mines. Some versions may automatically flag these spaces once all other squares in the game window have been unrevealed by the player, or reveal them once all flags have been placed.

Computational complexity

In 2000, Richard Kaye published a proof that it is NP-complete to determine whether a position in a Minesweeper game is consistent with some placement of mines.[5]

Measuring board difficulty

The difficulty of a given minesweeper board is often measured using the 3BV measure (stands for Bechtel's Board Benchmark Value).

Method

The 3BV of a board is the total count of:

For example, in the illustrated example, there is one opening (shown by white borders) and there are seven further numbered squares (green dots), giving a 3BV rating of 8. Equivalently, it is the minimum number of clicks required in typical implementations to reveal all of the mine-free squares.

3BV/s

3BV/s stands for 3BV per second.

Because the time that is needed to finish a Minesweeper board depends highly on the difficulty of the board, it may not be the best way to compare records. 3BV/s on the other hand does consider the difficulty of the Minesweeper board as well as the time needed to finish it. Among the best Minesweeper players, 3BV/s records are not nearly as important as time records, but they give a picture of how fast someone can play with regard to mouse-handling.

If flags are marked, it is possible to require fewer clicks than the 3BV of the respective board. Using only left clicks is called non-flagging (nf) whereas marking mines with right-clicks is called flagging-style.

Criticism

In 2001, the Italian "International Campaign to Ban Winmine" voiced strong concern over the game, contending that it is an "offense against the victims of the mines" and those who risk their lives to clear them. They created their own "Winflower" game, and lobbied Microsoft to use it in place of Minesweeper in Windows 98.[6] As a reaction to this criticism, the version of Minesweeper included in Windows Vista and Windows 7 offers a mode in which the mines are replaced with flowers.[7]

See also

Notes

  1. ^ http://it.wikipedia.org/wiki/Campo_minato_(videogioco)
  2. ^ "Class sp.SinglePointStrategy". Ccs.neu.edu. http://www.ccs.neu.edu/home/ramsdell/pgms/doc/sp.SinglePointStrategy.html. Retrieved 2009-06-02. 
  3. ^ [1]
  4. ^ "440 Sample Questions". Cs.rutgers.edu. http://www.cs.rutgers.edu/~mdstone/class/440-fall-99/hw3.html#p3. Retrieved 2009-06-02. 
  5. ^ Kaye (2000)
  6. ^ Blincoe (2001)
  7. ^ Microsoft Shell Blog - The UI design minefield - er... flower field? at the Wayback Machine (archived January 19, 2008)

References

External links